MMR（Maximal Marginal Relevance）多样性算法在推荐系统中的作用是平衡推荐结果的相关性和多样性。推荐系统通常会根据用户的兴趣和历史行为推荐最相关的内容，但这样做可能会导致推荐内容过于相似，缺乏多样性。

MMR 会在每一步选择相关性高且与已选项相似度低的内容，从而在确保推荐结果与用户兴趣相关的同时，增加推荐结果的多样性。这种方法能有效避免推荐结果中的重复性，提高用户体验，使得推荐内容更丰富多样。

1. 基础算法

精排给 $n$ 个候选内容打分，记融合之后的分数为 $\text{reward}_1$，$\text{reward}_2$，…，$\text{reward}_n$，将第 $i$ 和 第 $j$ 个内容的相似度定义为 $\text{sim}(i, j)$。重排算法的目标是从 $n$ 个内容中选出 $k$ 个，既要有⾼精排分数，也要有多样性。

将已经选择的内容集合记为 $\mathcal{S}$，未选择的内容集合记为 $\mathcal{R}$，则集合 $\mathcal{R}$ 中每个内容 $i$ 的 Marginal Relevance 分数可以定义为：

\[\text{MR}_i = \theta \cdot \text{reward}_i - (1 - \theta) \cdot \max_{j \in \mathcal{S}} \text{sim}(i, j)\]

其中：

  • $-\max_{j \in \mathcal{S}} \text{sim}(i, j)$ 表示内容 $i$ 和已选择的内容的相似度，可以理解为内容 $i$ 的多样性分数，取负号是为了让相似度越小，分数越高。

  • $\theta$ 是一个超参数，用来调节精排分数和多样性分数的权重。$\theta$ 越大，越偏向于选择精排分数高的内容，$\theta$ 越小，越偏向于选择多样性高的内容。

基础 Maximal Marginal Relevance（MMR）算法的步骤如下：

  1. 已选择的内容集合 $\mathcal{S} = \emptyset$，未选择的内容集合 $\mathcal{R} = {1, 2, …, n}$

  2. 选择精排分数最高的内容 $i^* = \arg \max_{i \in \mathcal{R}} \text{reward}_i$，将其移动到 $\mathcal{S}$ 中

  3. 做 $k - 1$ 次循环：

    a. 计算集合 $\mathcal{R}$ 中每个内容 $i$ 的 Marginal Relevance 分数 $\text{MR}_i$

    b. 选择 Marginal Relevance 分数最高的内容 $i^* = \arg \max_{i \in \mathcal{R}} \text{MR}_i$，将其移动到 $\mathcal{S}$ 中

算法执行完毕后，$\mathcal{S}$ 中的内容即为最终的推荐结果，一共 $k$ 个。

下面是一个简单的 Python 代码实现，用 26 个大写字母代替待推荐的内容，最开始时随机为他们赋一个精排分数（相关性分数）。

import random
import string

# Mapping of characters to scores
score = {c: random.random() for c in string.ascii_uppercase}

# Print the ranked list
sorted_items = sorted(score.items(), key=lambda x: x[1], reverse=True)
for pos, item in enumerate(sorted_items, 1):
  print(pos, item[0], item[1])

同时定义不同字母之间的相似度（多样性分数）为两个字母的 ASCII 值的差的绝对值除以 26。

def similarity(a: str, b: str) -> float:
  """
  Calculate the similarity between two characters.

  Args:
    a (str): The first character.
    b (str): The second character.

  Returns:
    float: The similarity between the two characters, ranging from 0 to 1.
  """
  # Calculate the absolute difference between the ASCII values of the two characters
  diff = abs(ord(a) - ord(b))

  # Calculate the similarity by dividing the difference by the maximum possible difference
  similarity_score = 1 - diff / 26

  return similarity_score

则基础 MMR 算法可以实现如下（假设最终需要输出 $k=10$ 个推荐内容）：

def rank(theta=0.7):
  """
  Rank items using a score-based algorithm.

  Args:
    theta (float): The weight for the item's score.

  Returns:
    list: The ranked list of items.
  """
  selected_items = []
  candidate_items = list(score.keys())

  for pos in range(10):
    if pos == 0:
      # Select the item with the highest score as the first item
      item = max(candidate_items, key=lambda x: score[x])
      selected_items.append(item)
      candidate_items.remove(item)
      continue

    # Calculate the margin relevance for each candidate item
    margin_relevance = {
      i: theta * score[i] - (1 - theta) * max(similarity(i, j) for j in selected_items)
      for i in candidate_items
    }

    # Select the item with the highest margin relevance
    item = max(candidate_items, key=lambda x: margin_relevance[x])
    selected_items.append(item)
    candidate_items.remove(item)

  return selected_items

2. 滑动窗口

标准的 MMR 算法可以记作：

\[\text{MMR}(\mathcal{R}, \mathcal{S}) = \underset{i \in \mathcal{R}}{\operatorname{argmax}}\left\{\theta \cdot \operatorname{reward}_i-(1-\theta) \cdot \max _{j \in \mathcal{S}} \operatorname{sim}(i, j)\right\}\]

在实际操作中可能存在如下问题：

  • 已选中的内容越多（即集合 $\mathcal{S}$ 越大），越难找到内容 $i \in \mathcal{R}$，使得 $i$ 和 $\mathcal{S}$ 中的内容都不相似。

  • 设 $\text{sim}$ 的取值范围是 $[0, 1]$。当 $\mathcal{S}$ 很大时，多样性分数 $\max _{j \in \mathcal{S}} \operatorname{sim}(i, j)$ 总是约等于 1，导致 MMR 算法失效。

解决方案： 设置一个滑动窗口 $\mathcal{W}$，比如最近选中的 10 个内容，用 $\mathcal{W}$ 代替 MMR 算法中的 $\mathcal{S}$。

滑动窗口的 MMR 算法可以记作：

\[\text{MMR}(\mathcal{R}, \mathcal{W}) = \underset{i \in \mathcal{R}}{\operatorname{argmax}}\left\{\theta \cdot \operatorname{reward}_i-(1-\theta) \cdot \max _{j \in \mathcal{W}} \operatorname{sim}(i, j)\right\}\]

基于滑动窗口的 MMR 算法可以有效解决多样性评分失效的问题，提高推荐结果的多样性，下方是一个简单的 Python 代码实现：

def rank_sliding_window(theta=0.7, window=4):
  """
  Rank items using a sliding window algorithm.

  Args:
    theta (float): The weight for the item's score.
    window (int): The size of the sliding window.

  Returns:
    list: The ranked list of items.
  """
  selected_items = []
  candidate_items = list(score.keys())

  for pos in range(10):
    if pos == 0:
      # Select the item with the highest score as the first item
      item = max(candidate_items, key=lambda x: score[x])
      selected_items.append(item)
      candidate_items.remove(item)
      continue

    # Calculate the margin relevance for each candidate item
    mr = {
      i: theta * score[i]
      - (1 - theta) * max(similarity(i, j) for j in selected_items[-window:])
      for i in candidate_items
    }

    # Select the item with the highest margin relevance
    item = max(candidate_items, key=lambda x: mr[x])
    selected_items.append(item)
    candidate_items.remove(item)

  return selected_items

3. 结合业务规则

重排除了要考虑多样性之外，有时候需要同时满足一些业务规则。以下是在 UGC 内容社区推荐场景下的一些规则举例：

  1. 规则 1： 一次曝光中，最多同时出现 $k$ 个同类型物料

    这里的物料“类型”指的是：图文物料 或 视频物料。例如当 $k=5$ 时，最多连续出 5 个图文/视频物料。如果排在第 $i$ 到 $i+3$ 的都为视频物料，那么第 $i+4$ 个物料必须为图文物料。

  2. 规则 2： 每 $k$ 个物料最多出现 1 个运营推广物料

    运营推广物料的精排分会乘以大于 1 的系数（boost），帮助这类物料获得更多曝光。为了防止 boost 影响用户体验，限制每 $k=4$ 个物料最多出现 1 个运营推广物料。如果排第 $i$ 位的是运营推广物料，那么排 $i+1$ 到 $i+3$ 的不能是运营推广物料。

  3. 规则 3： 前 $t$ 个物料最多出现 $k$ 个带电商内容的物料

    排名前 $t$ 的物料最容易被看到，对用户体验最重要（一般 top 4 为首屏）。例如，限制：前 $t=1$ 个物料最多出现 $k=0$ 个带电商内容的物料，前 $t=4$ 个物料最多出现 $k=1$ 个带电商内容的物料。

接下来介绍如何将业务规则融入到前面介绍的 MMR 算法中。

根据上文的介绍，MMR 算法每一轮都会从候选集 $\mathcal{R}$ 选出一个内容。为了满足业务规则，我们可以在每一轮计算候选集 $\mathcal{R}$中的每个内容的 Marginal Relevance 分数 $\text{MR}_i$ 前，先用这些规则排除掉部分内容 $\mathcal{R}$ 中的部分内容，得到子集 $\mathcal{R’}$。用 $\mathcal{R’}$ 代替 $\mathcal{R}$，再执行 MMR 算法，则选中的内容都符合规则。

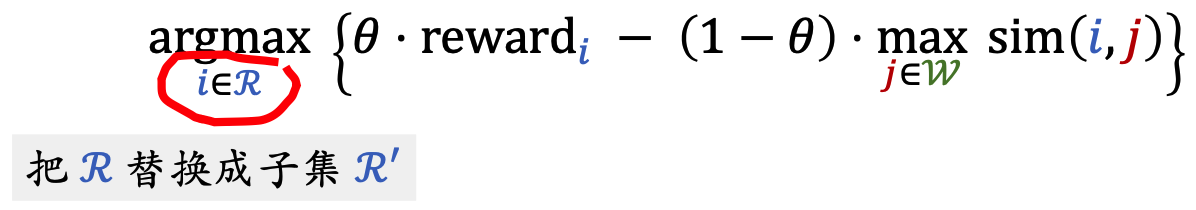
下方是一个简单的 Python 代码实现：

def rank_sliding_window_with_rule(theta=0.7, window=4):
  """
  Rank items using a sliding window algorithm and a filtering rule.

  Args:
    theta (float): The weight for the item's score.
    window (int): The size of the sliding window.

  Returns:
    list: The ranked list of items.
  """
  selected_items = []
  candidate_items = list(score.keys())

  for pos in range(10):
    # If it's the first position, select the item with the highest score
    if pos == 0:
      item = max(candidate_items, key=lambda x: score[x])
      selected_items.append(item)
      candidate_items.remove(item)
      continue

    # Apply the filtering rule to exclude items that do not meet the condition
    new_R = [i for i in candidate_items if score[i] > 0.5]

    # !NOTE: The new candidate set may be empty after filtering
    if not new_R:
      # TODO: Add downgraded items to the candidate set
      ...

    # Calculate the margin relevance for each candidate item
    mr = {
      i: theta * score[i]
      - (1 - theta) * max(similarity(i, j) for j in selected_items[-window:])
      for i in new_R
    }

    # Select the item with the highest margin relevance
    item = max(new_R, key=lambda x: mr[x])
    selected_items.append(item)
    candidate_items.remove(item)

  return selected_items

4. 参考资料

  1. https://github.com/wangshusen/RecommenderSystem（本文图片均来自此repo）