推荐系统召回算法：Swing算法

Swing 算法广泛用于推荐系统的召回阶段，本文将介绍 Swing 算法的原理和实现。

ItemCF 算法可能存在的一个问题

ItemCF 算法在计算两个物品的相似性时认为：两个物品的受众重合度越大，两个物品的相似度越大。但是这种假设在实际应用中可能存在“小圈子”问题，举例来说：当两个不太相似的物品被转发到同一个微信群中时，这两个物品同时被群友点击，这样就会导致这两个物品的相似度很高，但是这两个物品实际上并不相似。

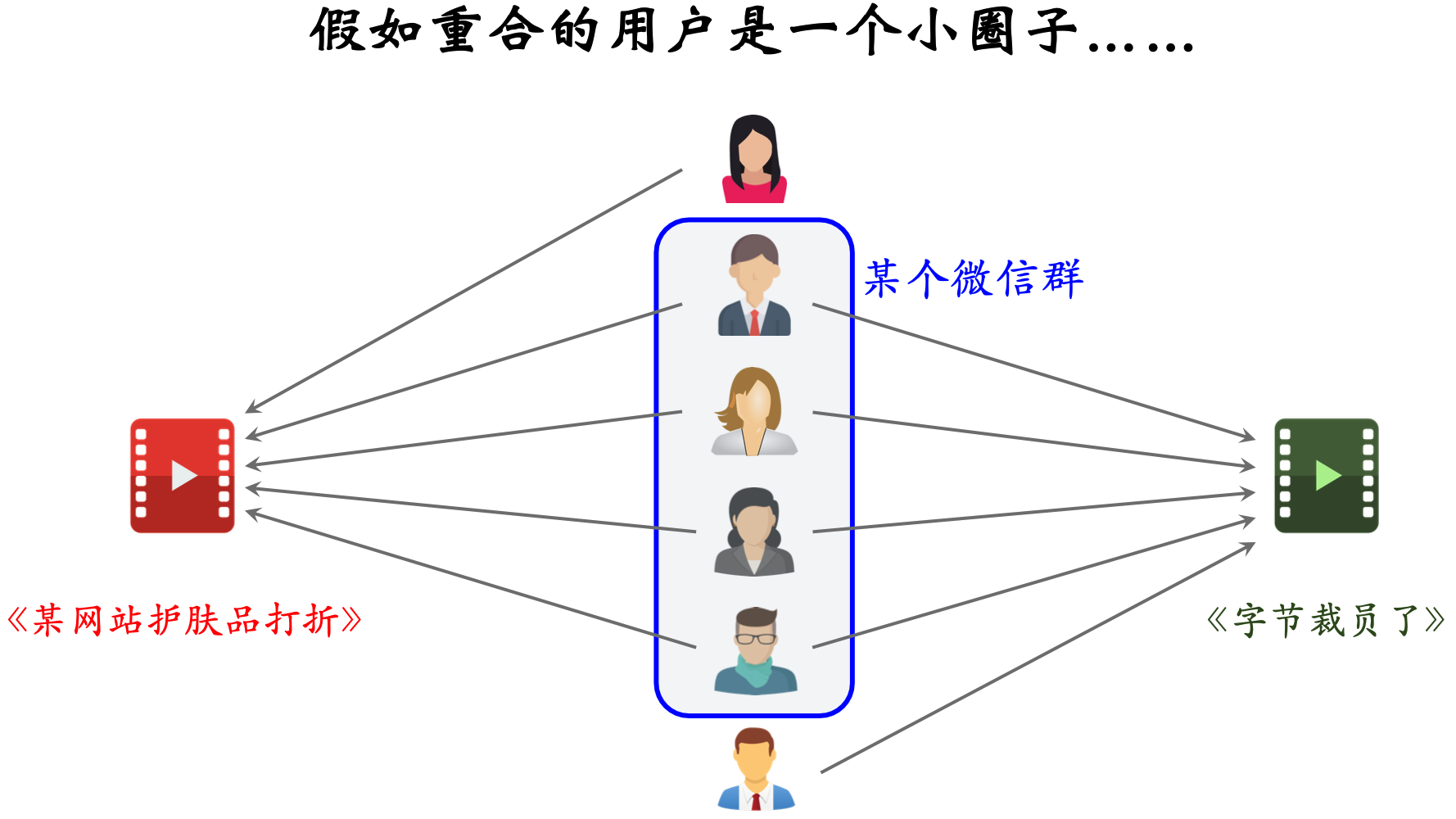
Swing 算法

Swing 算法的基本思想是：如果大量用户同时喜欢两个物品，且这些用户之间的重合度很低，那么这两个物品一定很相似。

将用户 $u_1$ 和用户 $u_2$ 喜欢的物品集合分别记为 $J_1$ 和 $J_2$，则两个用户的重合度 $overlap(u_1,u_2)$ 定义为：

$$overlap(u_1,u_2)=|J_1\cap J_2|$$

如果 $u_1$ 和 $u_2$ 的重合度很高，则他们可能来自于同一个小圈子，需要降低他们的权重。

将喜欢物品 $i_1$ 和喜欢物品 $i_2$ 的用户集合分别记为 $W_1$ 和 $W_2$，他们的交集 $V=W_1\cap W_2$，则两个物品的相似度 $sim(i_1,i_2)$ 定义为：

$$sim(i_1,i_2)=\sum _{u_1\in V}\sum _{u_2\in V}\frac{1}{\alpha +overlap(u_1,u_2)}$$

其中 $\alpha$ 是平滑项，可以避免分母为零，可以取一个较小的正数，例如 1。

Swing 算法在实际应用中的完整流程与 ItemCF 算法类似，只是在计算物品相似度时使用了 Swing 算法的公式。

总结

1. Swing 算法与 ItemCF 算法的唯一区别在于计算物品相似度的公式不同。
2. ItemCF 算法：两个物品的受众重合度越大，两个物品的相似度越大。
3. Swing 算法：额外考虑了重合用户是否来自于一个小圈子，如果是，则降低这些用户的权重。

参考资料

1. https://arxiv.org/pdf/2010.05525.pdf
2. https://github.com/wangshusen/RecommenderSystem（本文图片均来自此repo）