推荐系统召回算法：基于物品的协同过滤（ItemCF）

算法原理

如果用户喜欢物品 A，而物品 A 和物品 B 有很高的相似度，那么用户很有可能也喜欢物品 B。这就是基于物品的协同过滤（ItemCF）算法的基本思想。

例如，某位用户喜欢看《三国演义》，而《三国演义》和《水浒传》有很高的相似度，那么这位用户很有可能也喜欢看《水浒传》，如果用户没有看过《水浒传》，那么我们就可以推荐给用户看《水浒传》。

那么，推荐系统如何知道《三国演义》和《水浒传》有很高的相似度呢？思路：看过《三国演义》的用户，有多少人也看过《水浒传》？给《三国演义》好评的用户，有多少人也给《水浒传》好评？

算法实现

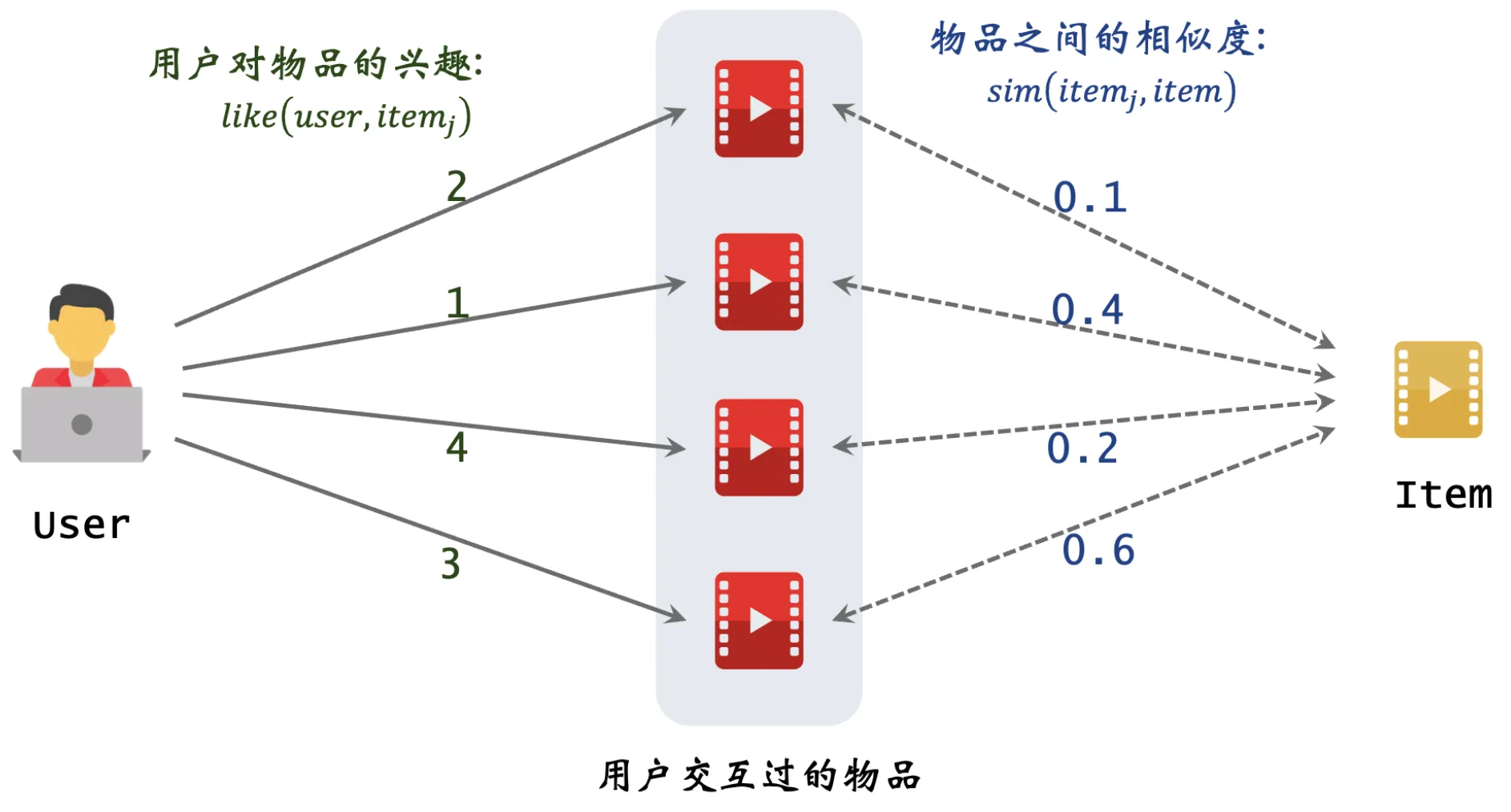
如上图所示，根据用户的历史行为日志，可以得到用户对部分已读物品的喜好程度（例如：点击记 1 分，点赞记 2 分，收藏记 3 分）。假设此时已知任意两个物品之间的相似度，那么我们可以结合两者预估用户对于每个候选物品的喜好程度。然后根据用户对候选物品的喜好程度，对候选物品进行排序，将排序靠前的物品推荐给用户。

用户对每个候选物品的喜好程度，可以通过下面的公式计算：

$$\sum _{j}like(user,ite{m}_j)\times sim(ite{m}_j,item)$$

其中，$like(user,ite{m}_j)$ 表示用户对物品 $ite{m}_j$ 的喜好程度，$sim(ite{m}_j,item)$ 表示物品 $ite{m}_j$ 和物品 $item$ 的相似度。

根据上面的公式，我们可以预估上图中用户对候选物品 item 的喜好程度：

$$2\times 0.1+1\times 0.4+4\times 0.2+3\times 0.6=3.2$$

物品相似度的计算

基于物品的协同过滤算法在计算物品相似度时的基本思想是：如果两个物品的受众有很多重合，那么这两个物品就很相似。例如，喜欢《三国演义》的读者和喜欢《水浒传》的读者重合度很高，那么《三国演义》和《水浒传》就很相似。

下面两张图片分别展示了两个物品的受众重合度，其中前者是两个物品不相似的情况，后者是两个物品相似的情况。

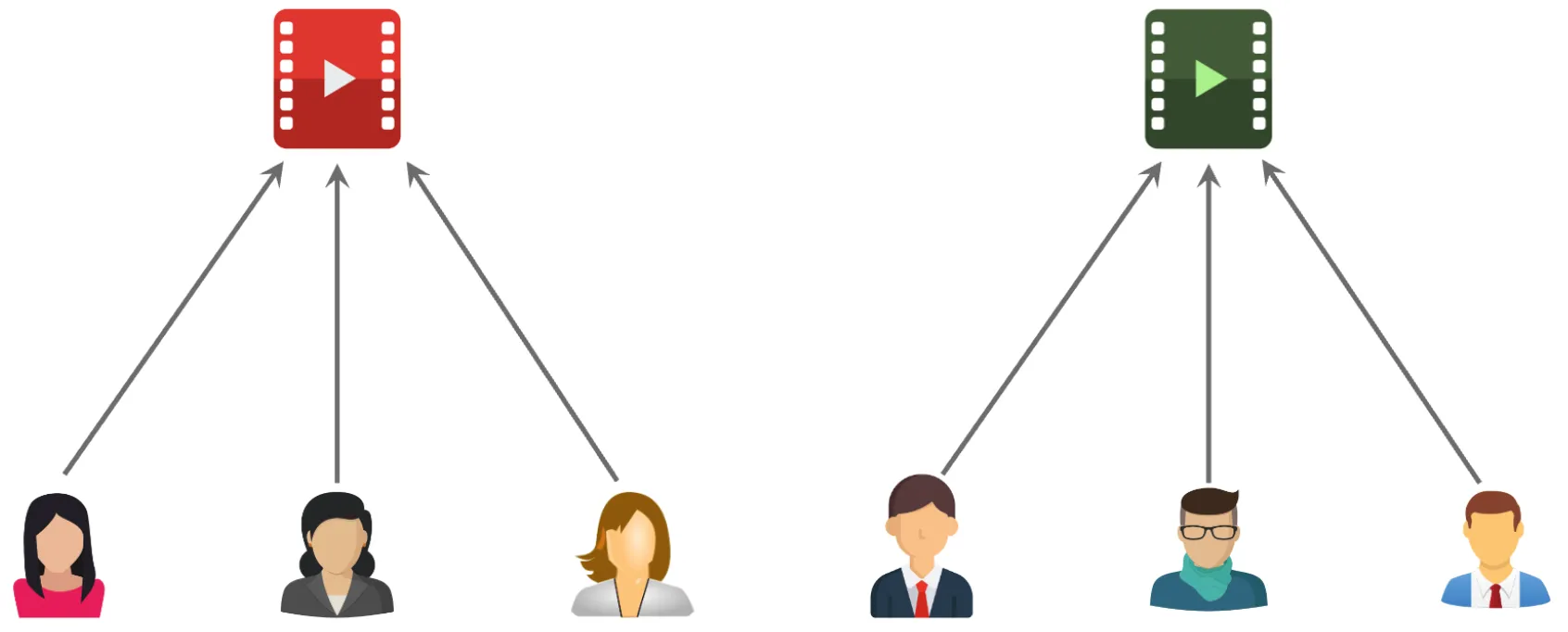
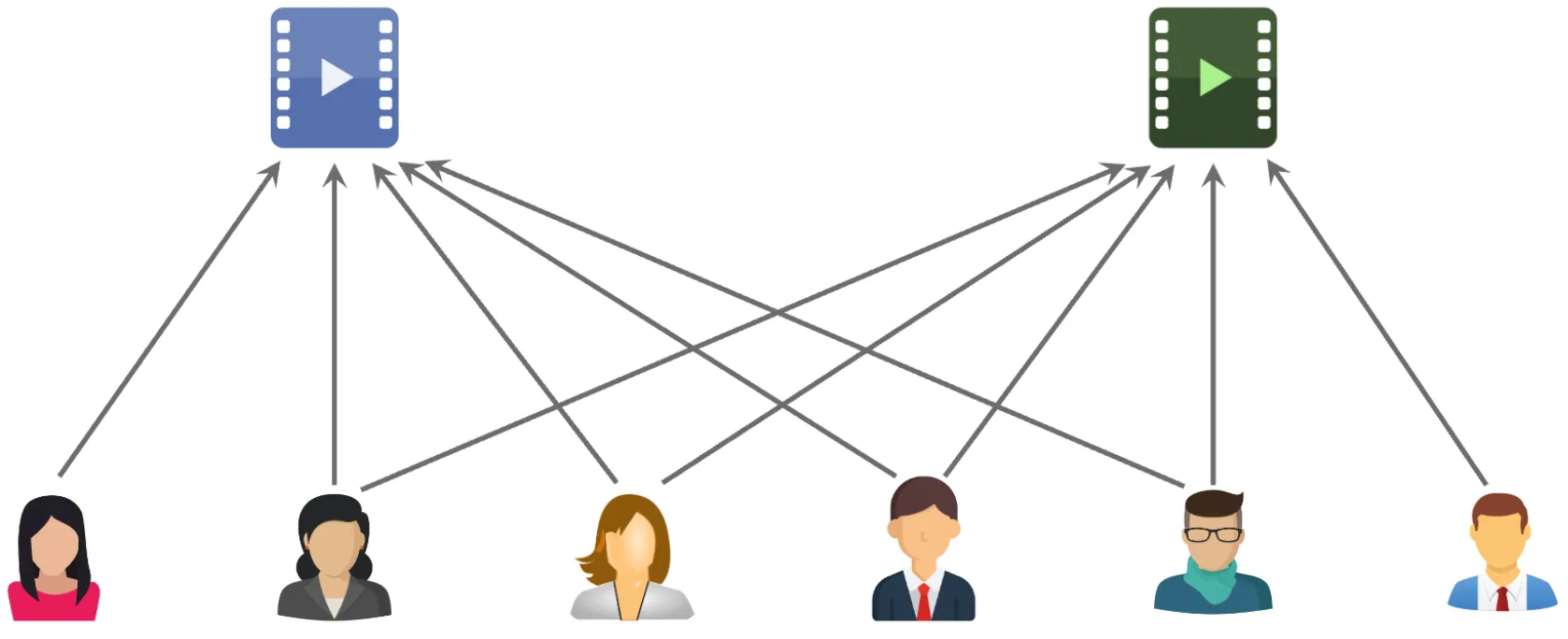
接下来介绍如何量化物品的相似度。假设喜欢物品 $i_1$ 的用户集合为 $W_1$，喜欢物品 $i_2$ 的用户集合为 $W_2$，$W_1$ 和 $W_2$ 的交集记为 $V=W_1\cap W_2$，那么物品 $i_1$ 和物品 $i_2$ 的相似度可以通过下面的公式计算：

$$sim(i_1,i_2)=\frac{|V|}{\sqrt{|W_1|\cdot |W_2|}}$$

其中，$|V|$ 表示 $V$ 的元素个数，$|W_1|$ 表示 $W_1$ 的元素个数，$|W_2|$ 表示 $W_2$ 的元素个数。这样计算出来的物品相似度介于 0 和 1 之间，值越大表示物品越相似。

这种计算物品相似度的方法没有考虑到用户对物品的喜好程度，只考虑了用户是否喜欢物品。如果需要考虑到用户对物品的喜好程度，可以通过余弦相似度来计算物品的相似度。

$$sim(i_1,i_2)=\frac{\sum _{v\in V}like(v,i_1)\times like(v,i_2)}{\sqrt{\sum _{u_1\in W_1}like(u_1,i_1{)}^2}\cdot \sqrt{\sum _{u_2\in W_2}like(u_2,i_2{)}^2}}$$

除了余弦相似度，还有一种计算物品相似度的方法，叫做皮尔逊相关系数。皮尔逊相关系数的计算公式如下：

$$sim(i_1,i_2)=\frac{\sum _{v\in V}(like(v,i_1)-\overline{like}(i_1))\times (like(v,i_2)-\overline{like}(i_2))}{\sqrt{\sum _{u_1\in W_1}(like(u_1,i_1)-\overline{like}(i_1){)}^2}\cdot \sqrt{\sum _{u_2\in W_2}(like(u_2,i_2)-\overline{like}(i_2){)}^2}}$$

其中，$\overline{like}(i)$ 表示物品 $i$ 的平均喜好程度。皮尔逊相关系数通过减去物品的平均喜好程度，可以消除物品的平均喜好程度对相似度的影响（消除物品评分偏差对结果的影响）。

还有一种皮尔逊相关系数的变种：

$$sim(i_1,i_2)=\frac{\sum _{v\in V}(like(v,i_1)-\overline{like}(v))\times (like(v,i_2)-\overline{like}(v))}{\sqrt{\sum _{u_1\in W_1}(like(u_1,i_1)-\overline{like}(u_1){)}^2}\cdot \sqrt{\sum _{u_2\in W_2}(like(u_2,i_2)-\overline{like}(u_2){)}^2}}$$

其中，$\overline{like}(v)$ 表示用户 $v$ 的平均喜好程度。这种皮尔逊相关系数的变种通过减去用户的平均喜好程度，可以消除用户的平均喜好程度对相似度的影响（消除用户评分偏差对结果的影响）。

在实际应用中的完整流程

ItemCF 算法在实际召回应用中，我们需要事先建立两个索引表：

• 用户-物品表：记录每个用户最近点击交互过的物品列表，以及每个物品的喜好程度，根据时间倒序排列，取前 $n$ 个物品。
• 物品-物品表：记录每个物品与其相似的物品列表以及相似度，根据相似度倒序排列，取前 $k$ 个相似物品。

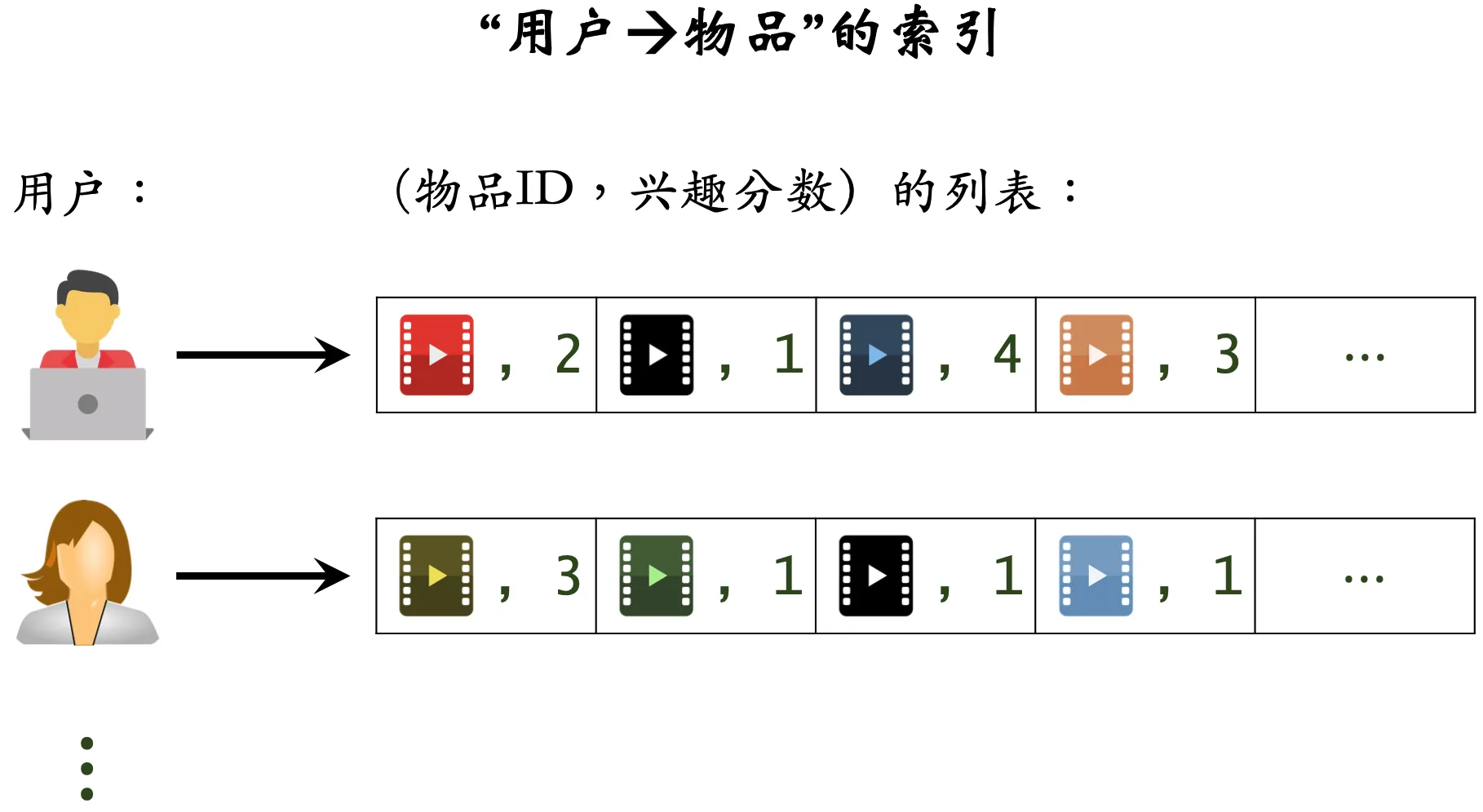
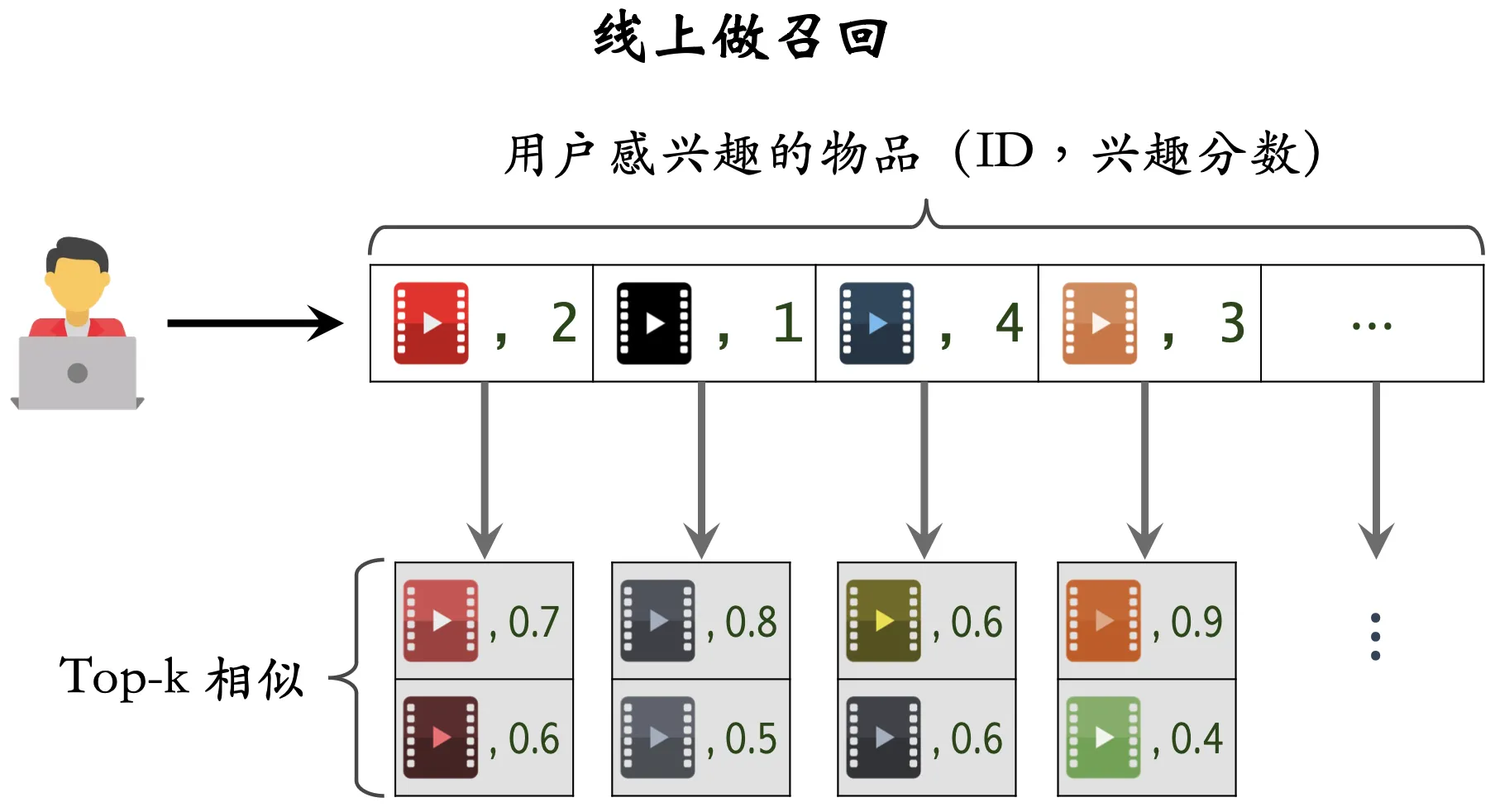
在线上实际应用中，我们可以通过“用户-物品表”来获得用户近期感兴趣的物品列表（last-n-items），然后通过“物品-物品表”来获得这些物品的相似物品列表（top-k-items），然后再根据公式预估用户对取回的这 $nk$ 个物品每兴趣分数，最后将分数最高部分物品推荐给用户（例如 Top100）。

总结

1. ItemCF 算法的基本思想是：如果用户喜欢物品 A，那么用户也很可能喜欢与物品 A 相似的物品 B。

2. 计算物品相似度：
   • 如果两个物品的受众有很多重合，那么这两个物品就很相似。

   • 只考虑用户是否喜欢物品，不考虑用户对物品的喜好程度：

     $$sim(i_1,i_2)=\frac{|V|}{\sqrt{|W_1|\cdot |W_2|}}$$

   • 基于余弦相似度计算物品相似度时，考虑到了用户对物品的喜好程度：

     $$sim(i_1,i_2)=\frac{\sum _{v\in V}like(v,i_1)\times like(v,i_2)}{\sqrt{\sum _{u_1\in W_1}like(u_1,i_1{)}^2}\cdot \sqrt{\sum _{u_2\in W_2}like(u_2,i_2{)}^2}}$$

   • 皮尔逊相关系数和皮尔逊相关系数的变种，通过减去物品的平均喜好程度或者用户的平均喜好程度，可以消除物品评分偏差或者用户评分偏差对相似度的影响：

     $$sim(i_1,i_2)=\frac{\sum _{v\in V}(like(v,i_1)-\overline{like}(i_1))\times (like(v,i_2)-\overline{like}(i_2))}{\sqrt{\sum _{u_1\in W_1}(like(u_1,i_1)-\overline{like}(i_1){)}^2}\cdot \sqrt{\sum _{u_2\in W_2}(like(u_2,i_2)-\overline{like}(i_2){)}^2}}$$ $$sim(i_1,i_2)=\frac{\sum _{v\in V}(like(v,i_1)-\overline{like}(v))\times (like(v,i_2)-\overline{like}(v))}{\sqrt{\sum _{u_1\in W_1}(like(u_1,i_1)-\overline{like}(u_1){)}^2}\cdot \sqrt{\sum _{u_2\in W_2}(like(u_2,i_2)-\overline{like}(u_2){)}^2}}$$
3. 线上做召回：
   • 维护两个索引表：用户-物品表（用户最近交互过的 $n$ 个物品列表）和物品-物品表（相似度最高的 $k$ 个物品列表）。
   • 利用两个索引表，每次返回分数最高的 $n\times k$ 个物品。

   • 预估用户对物品的喜好分数：

     $$score(u,i)=\sum _{i^{\prime }\in top-k-items(i)}like(u,i^{\prime })\times sim(i,i^{\prime })$$
   • 返回用户喜欢的物品列表（例如 Top100），作为召回结果。

参考资料

1. https://github.com/wangshusen/RecommenderSystem（本文图片均来自此repo）
2. 王哲《深度学习推荐系统》